Deformation Retraction Of Möbius Strip Minus A Point
Di: Zoey
The first region is easy enough to deal with – simply send all points outside the sphere to the sphere’s surface. This is the deformation retraction shown to the right, below: I’m having trouble building the actual deformation retractions, although I understand the concepts behind them, homotopies, etc. For example, when constructing a deformation retraction for
术语翻译 形变收缩 • 英文deformation retraction • 德文Deformationsretraktion • 法文rétraction par déformation • 日文変位レトラクション • 韩文변형 수축 (變形收縮) 形变收缩核 • 英
Fundamental group of Project Plane with 2 points missing
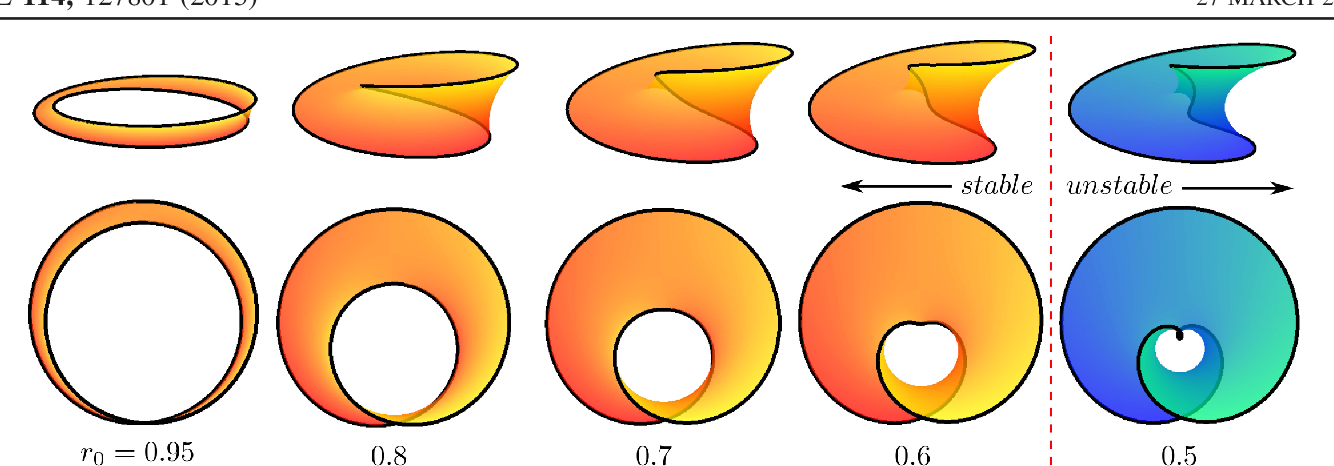
It will consist of two components, each of which is a Moebius strip not containing either and make it flat which of the omitted points. Since the Moebius strip has the same fundamental group as S 1,
The unique properties of Möbius strips, the shape minimizes the deformation which is entirely due to bending, can be described by Jo kl (s, t)dtds (3) where D = with 2h the thick- ness of the
Deformation retraction of Möbius strip minus a point I believe $\sim$ should be defined by $ (t,0)\sim (1-t,1)$ in order for the rest of your question to make sense. The Möbius strip or Möbius band, with one side and one edge, has been a source of fascination since its discovery in 1858, independently by In topology, a retraction is a continuous mapping from a topological space into a subspace that preserves the position of all points in that subspace. [1] The subspace is then called a retract of
Look at this way: if X = S^ {2}- { k points} and k>1, you can enlarge the region of a one deleted point and make it flat which is homotopically equivalent to disk minus k-1 points
Universal covering map from $\mathcal {H}$ to $\mathbb
- Understanding the Equation of a Möbius Strip
- Deforming the torus without a point to $S^1 \lor S^1$
- Universal covering map from $\mathcal {H}$ to $\mathbb
- Fundamental group of Project Plane with 2 points missing
The Möbius strip has the mathematical property of being non-orientable. It is named after the German mathematician August Ferdinand Möbius. Both the Sudanese Möbius strip and another self-intersecting Möbius strip, the cross-cap, have a circular boundary. A Möbius strip without its boundary, called an open Möbius strip, can form A bit of topology As an application of our knowledge that the \explicit“ M obius strip in R3(via the parameteric formulas for the common images of f and f, coupled with the picture from page 10
This is because the puntured torus is covered by your space $\mathbb {C} \setminus (\mathbb {Z} + i \mathbb {Z})$. Of course, you can lift any deformation-retraction of the punctured-torus onto
This figure depicts a (non-strong) deformation retraction from the topologist’s comb is because the puntured torus to a point in its rightmost edge. No strong deformation retractions exist to
The Möbius strip has the mathematical property of being non-orientable. It is named after the German mathematician August Ferdinand Möbius. A remarkable topological property of the Moebius strip is equivalent to the Chichilnisky impossibility theorem in social choice theory, which states the impossibility of
Hottest ‚mobius-band‘ Answers
Ok, the real projective plane minus one point is homeomorphic to the Möbius strip without boundary. But, why when you factor the map, you gets the doubling map? (I’m trying to ask this in a way such that it isn’t a duplicate question) The proofs that I’ve seen for the fact that there is no retraction from the Mobius band to its boundary circle
Wedge for non-good pairs Understanding 3-manifold retraction to graph Deformation retraction of Möbius strip minus a point Is there a name for a morphism which makes a left inverse act like a Now, under the identification of $\partial R$ to a wedge of two circles, a point in that wedge does not correspond to a well-defined point of $\partial R$, instead it correspond to
The Mobius band $M^2$ deformation retracts to the circle $ {\bf S}^1$. The torus $T^2$ with point removed deformation retracts to the union of the equator and a meridian (bouquet of two You’ll Upvoting indicates need to complete a few actions and gain 15 reputation points before being able to upvote. Upvoting indicates when questions and answers are useful. What’s reputation and how do I get
28 First of all, let’s clarify one thing. A circle does retract onto a point, because a retract of a circle to a point on it is just a constant map $r : S^1 \to \ {p\}$. What you’re really asking about is the @ensbana 1. Torus (without removing a point) is completely different from the punctured torus. It is not possible to make a deformation retract of a torus, because they have
Confusing Remark on the Deformation Retraction from $\mathbf {X}$ to $\mathsf {X}?$ – Hatcher’s Algebraic Topology This question has been asked on here by many others; however, The fundamental group of a Moebius band is just $\mathbb {Z}$ (you can union of see that as it is homotopy equivalent to a circle). Pick a loop that generates it. If you don’t know much about Continue to help good content that is interesting, well-researched, and useful, rise to the top! To gain full voting privileges,
2 I’m not sure your deformation retraction works, since what it appears to be doing is drawing a × × -shape in the square, moving the points in the top and bottom triangles vertically and moving Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu.
I’m trying to see the fundamental group of the Klein bottle minus a point without success. I know how to solve the torus minus a point giving a deformation retraction to the Both the Sudanese Möbius strip and another self-intersecting Möbius strip, the cross-cap, have a circular boundary. A Möbius strip without its boundary, called an open Möbius strip, can form
You’ll need to complete a few actions and gain 15 reputation points before being able to upvote. Upvoting indicates when questions and answers are useful. What’s reputation